Sr. No
Fine topology
Homeomorphism group
Topological properties
1
Zeeman topology 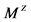 (1967): Finest topology which induces three dimensional Euclidean topology on every space-axis and one dimensional Euclidean topology on every time-axis
(1967): Finest topology which induces three dimensional Euclidean topology on every space-axis and one dimensional Euclidean topology on every time-axis
G = Lorentz group with translations and dilatations
Dossena (2007): neither locally compact nor Lindelof, not normal, separable but not first countable, path-connected but not simply connected
2
s-topology : Nanda (1971): Finest topology which induces three dimensional Euclidean topology on every space-like hypersurface
: Nanda (1971): Finest topology which induces three dimensional Euclidean topology on every space-like hypersurface
G
G.Agrawal and S. Shrivastava (2012): separable, first countable, path-connected, not regular, not metrizable, not second countable, noncompact, and non-Lindelof, not simply connected
3
t-topology : Nanda (1972): Finest topology which induces one dimensional Euclidean topology on every time-like line
: Nanda (1972): Finest topology which induces one dimensional Euclidean topology on every time-like line
G
G.Agrawal and S. Shrivastava (2009): separable, first countable, path-connected, not regular, not metrizable, not second countable, not locally compact, not simply connected
4
A-topology : Nanda (1979): Finest topology which induces one dimensional Euclidean topology on every time-like line and light-like line and three dimensional Euclidean topology on every space-like hypersurface
: Nanda (1979): Finest topology which induces one dimensional Euclidean topology on every time-like line and light-like line and three dimensional Euclidean topology on every space-like hypersurface
G
G.Agrawal and Soami Pyari Sinha (2014): separable, not first countable, connected and path-connected, not normal, not metrizable, Not comparable with t-topology nor with s-topology
5
Fine topologies 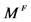 by Williams (1974): Finest topology which induces one dimensional Euclidean topology on every time-like line and space-like line
by Williams (1974): Finest topology which induces one dimensional Euclidean topology on every time-like line and space-like line
Conformal group of Minkowski space whose 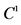 subgroup is G
subgroup is G
Hausdorff, separable, first countable, but not regular and hence not metrizable
6
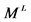 : Finest topology which induces one dimensional Euclidean topology on every straight line
: Finest topology which induces one dimensional Euclidean topology on every straight line
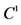 homeomorphisms form projective group generated by full linear group and translations
homeomorphisms form projective group generated by full linear group and translations
Weaker than 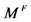 and
and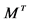 , Hausdorff, separable and first countable, not regular and hence not metrizable
, Hausdorff, separable and first countable, not regular and hence not metrizable