Exposition of condition 1
The social welfare function is defined for every admissible pair of individual orderings, R1, R2.
In all possible choices, there must be a set S composed of three choices, which satisfies the conditions below: for any individual ordering T1,・・・, Tn of objects in S, there is an admissible individual ordering set R1,・・・, Rn for all objects, such that for every individual i, and all x, y in S, we have xRiy if and only if xTiy.
Exposition of condition 2
If an alternative social state x arises or does not fall in the ordering of each individual without any other change in those orderings and if x was preferred to another alternative y before the change in individual orderings, then x is still preferred to y.
Let R1,・・・, Rn and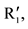
・・・, 
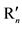be two sets of individual orderings, R and Rʹ be the corresponding social ordering relationship, P and 
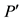be the corresponding social preferences relationship. Suppose for individual i the two ordering relationships have the following connection: (1) for any two options x' and y' different from option x, x'R'iy' if and only if xRiy'; (2) for any y', if xRiy', then xR'iy'; For any y', if xPiy', then xP'iy'. Then, if xPy, then xP'y.
Exposition of condition 3
(Independence of irrelevant alternatives). Let R1, R2, and be two sets of individual orderings. If for both individuals i and for all x and y in a given set of alternatives S, xRiy if and only if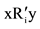
, then the social choice made from S is the same whether the individual orderings are R1, R2, or 
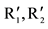(the author notes: this condition is known as the “independent candidate independence” conditions)
Let R1, R2, and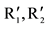 
be two sets of individual orderings, C(S) and C'(S) be the corresponding social choice functions. If for some given environment S, for all individual i and all elements x and y, if the sufficient and necessary condition for xRiy is xR'iy, then the same is true for C(S) and C'(S) (i.e. independence or uncorrelatedness).
Exposition of condition 4
The social welfare function is not to be imposed.
Definition 5: if for two different objects x and y, and for any individual ranking set R1,・・・, Rn, we have xRy, then we call the social welfare function to be imposed.
Condition 4: social welfare function is not imposed.
Exposition of condition 5
(Non-dictatorship). The social welfare function is not to be dictatorial (non-dictatorial).
Definition 6: if there is some individual i, such that for any x and y, and for any ordering R1, Rn of other individuals except i, xPiy implies xPy, then the social welfare function is called dictatorial.
Condition 5: Social welfare function is not arbitrary (i.e. social welfare function is authoritarian).