Gibbs/Metropolis-Hastings Sampler Algorithm
1) Initialize
, 
and
.
2) Based on Metropolis-Hastings, create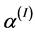 
using (28) with the 
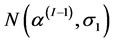proposal distribution, where 
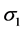is from variances-covariance matrix.
3) Based on Metropolis-Hastings, create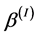 
using (29) with the 
proposal distribution, where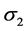 
is from variances-covariance matrix.
4) Based on Metropolis-Hastings, create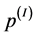 
using (30) with the 
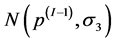proposal distribution, where 
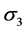is from variances-covariance matrix.
5) Calculate 
and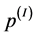
.
6) Put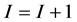 
.
7) Repeat steps (2 - 5) N times.
8) We get the point estimation by Bayes MCMC of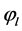 
(
and
) as
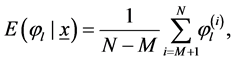(31)
where M is the number of iterations (burn-in period) before the stationary distribution is accomplished and posterior variance of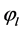 
becomes
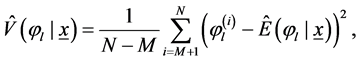(32)
9) The quintiles of the pattern are picked as the endpoints of the interval to calculate the reliable intervals of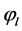
. Sort 
as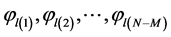 
. Hence, the symmetric credible interval with 
is
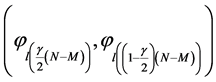(33)