Math Topic
Question Focus
Scenario Questions
Key Mathematics Ideas
Dividing Fractions
1.1: What does dividing fractions mean?
Imagine that you are teaching a group of sixth graders to solve the following problem:
A rope 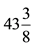 meters long is cut is cut into pieces which are each
meters long is cut is cut into pieces which are each  meters long. How many such pieces can we get out of the rope?
meters long. How many such pieces can we get out of the rope?
1.1 Describe how you would approach this problem with your students in a way that builds on their prior mathematical knowledge and/or skills related to division of whole numbers.
1.2 Suppose your answer is 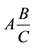 where A, B, and C are whole numbers so that 0 < B < C. How would you explain to students what the Ameans and what the
where A, B, and C are whole numbers so that 0 < B < C. How would you explain to students what the Ameans and what the 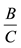 means?
means?
-Definitions of: whole numbers, fractions;
-Definitions of: dividing whole numbers, dividing fractions.
1.2: see 1.1
See above.
-Division as an alternative, but equivalent way of writing multiplication;
-Distributive law;
-Definition of mixed number;
-Representation using number line.
1.3: Why invert and multiply when dividing fractions?
1.3 Imagine that one of your sixth graders missed your lesson on fraction division. He studies the textbook and attempts the homework on his own. The next day he comes and tells you,
“The book says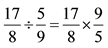 , but I don’t understand why.” How would you respond to this student?
, but I don’t understand why.” How would you respond to this student?
-Definition of dividing fractionsàwhy invert & multiply?
Linear Equation & Graph
2.1: What is the assumption or key mathematical concept underlying so-called proportional reasoning?
2.1 You are giving your seventh graders the district pre-algebra common assessment. One word problem on the assessment reads as follows:
“Abe is training for the Boston marathon, so he runs every day. This morning he ran 4 miles in 40 minutes. How many miles did he run in the first 20 minutes? Show your work.”
One of your top-performing students in the class, nicknamed “Einstein,” comes to you with her test and says, “There is not enough information given to solve this problem.”
1. How would you respond to “Einstein?”
2. Explain how you would teach the class about the critical mathematical concept (s) for solving this kind of word problem.
-Assumption: definition of constant rateàimplications for solving so-called proportional problems;
-Definition of division;
-Linear function without constant term (for higher grades).
2.2: See 2.1.
2.2 You are teaching a class of eighth graders and writing a test to assess their ability to translate word problems into symbolic equations. Come up with a story that could be represented by the equation: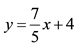 .
.
-Assumption: constant rate or speed.