Sequence of counters
The paper heuristically states that each synthetic sequence of natural numbers can be factorised. Into two sequences. One of these sequences is the sequence of counters. This sequence embodies the rules and it can be a selection of even any arbitrary operations. The simplest sequence of counters is that in which all the elements are unity.
Sequence of invariants
The paper heuristically states that each synthetic sequence of natural numbers can be factorised. Into two sequences. One of these sequences is the sequence of invariants. This sequence embodies the building blocks but organised in the manner of a sequence. The simplest sequence of invariants is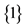 , which can be primed from: kernel:
, which can be primed from: kernel: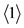 .
.
Sequence
A sequence of numbers is a collection of highly ordered set of individual numbers, each referred to as an element or a term, separated by a coma or space. A sequence is denoted by a curly bracket: .
.
The terms or elements of a sequence are either separated from one another by space or by a coma.
The terms sequence and series are not interchangeable in this paper.
Sequences of natural numbers
Natural numbers are a product of natural selection at the cultural level and without any real concern to mathematics. However, the sequence of natural numbers is a declaration to mathematise natural numbers. This paper shows that the sequence of natural numbers are themselves a synthesis, primed out of the kernel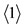 .
.
Series
It is a sequence with prescribed operation on all of its terms.
Size
The Size of a sequence/series is the number of elements in it and this is normally reflected in the ultimate term, often denoted by n. For an infinite sequence/series, the size is infinite but still its last term may be denoted as n to reflect the point of interest.
Space
Difference Table is broadly deciphered in terms of
1) Space: which refers to the horizontal layout of the elements of the parent sequences or their derivatives.
2) Zones: which refers to the diagonal layout of the sequences of counters.
Note that these terms are not deliberately in this paper.
Specification
The paper unravels that each synthetic sequence of natural numbers.
Although the operators for regeneration and raising to powers have not been presented yet, these two operations have a direct bearing on the order of a sequence. These three terms are not interchangeable, as each represents a specific concept. Arithmetic calculus proposes a notation for generation, degree and order of a sequence.
Synthetic sequences of natural numbers
The paper holds that there are countless sequences synthesised from the sequence of natural numbers.
Transitional Diagonal (TD)
Four TDs are distinguished and they are numbers in the reducemental direction:
TD1: delineates the trailing zone from the leading zone.
TD2: delineate the standard allele.
TD3: delineates the transition from convoluting zone to regenerating zone.
TD4: delineates the transition from the regenerating zone to the kernel, where there is no more sequence but plain building blocks.
Zone
Difference Table has many zones and these are delineated in Table 7.1 in generic terms. Each zone has been given a name and defined in this Glossary. A range of generic diagonals are distinguished in terms of Transitional Diagonals 1, 2, 3 and 4.