Direct product
This is defined by (4.2) and (4.3) in Section 4.2. It is denoted by two different approaches:
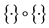 when the product are a sequence
when the product are a sequence 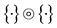 when the products are conducemental.
when the products are conducemental.
This may equally be called the dot product rule, as the symbols suggests.
Encapsulation
When a set of multiplication operation has been carried out, the emerging parent sequence encapsulates its inherent complexity. This can be analysed by reducemental analysis in terms of its order, which is composed of encapsulated degree, encapsulated generation. When a parent sequence is re-operated by multiplication, it creates layers of encapsulation. In general, reducemental analysis is capable of keeping the track of the last generation and degree.
Generation
Generation is an important dimension of arithmetic calculus and refers to the number of times that a sequence is regenerated.
Interoperability
Arithmetic calculus unearths a highly interoperable world of mathematics. The role of the sequences of counter is normally self-evident when the interconnectivity of one sequence is sought from another one. However, this is not so for the sequences of invariants. This leads to another set of very interesting operations, termed in the paper as interoperability.
Leading terms
Consider the finite sequence: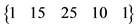 . Its first two terms are increasing towards a maximum and then dipping to a lower value again. The increasing terms are referred to as the leading terms and the dipping terms as the trailing terms.
. Its first two terms are increasing towards a maximum and then dipping to a lower value again. The increasing terms are referred to as the leading terms and the dipping terms as the trailing terms.
Leading zone
One of the zones among the many zones in Difference Table as delineated in Table 7.1 in generic terms. This is located on the reducemental direction of Transitional Diagonal 1.
Kernel
A kernel is not a sequence but the very final residue of a sequence when subjected to generations of reducement.
Kernels measure the complexity of a sequence.
Another term to kernel is building blocks.
Level
In combinatoric operator, the level refers to the finite and distinct objects, from which a smaller set is selected (this is referred to as the base).
Natural numbers
This is simply the numbers as used in natural language. They are 1, 2, 3, ×××
Order
The order of a combinatoric operator is the difference between its level and its base. It combined degree and generation, the three of which are the key for specifying a sequence.
Priming
Conversion of a kernel to a sequence, where the kernel is not a sequence yet.
Parent sequence
This is the top line in Difference Table.
Recursive sequences
Recursive sequences are incomplete sequences and often look like the work in hand but more is expected to be done.
Reducement
This term is introduced in this paper and is equivalent to differentiation.
Reducemental
This term is introduced in this paper and is equivalent to genetics of living things.
Reducemental analysis
This is equivalent to dimensional analysis in physical sciences. Through this analysis, an overarching view is taken of a sequence of natural numbers but the relevant analysis has not been detailed in this paper.
Regeneration
This is a variation of convolution, in which there is no dipping. The regeneration operator is defined by (4.6) in Section 4.1.2.
Regenerating Zone
This refers to alleles located between Transitional Diagonal 2 and 3.
In this zone, the size of the allele remain constant.
Regenerating product
This is defined by (4.4) in Section 4.3.
It is denoted by: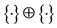 .
.